From closed chaotic to ordered spaces and viceversa.
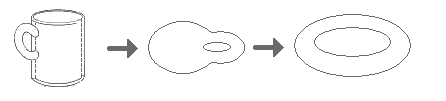
When some mathematical historians support that Henri Poincaré is one of the founders of the Topology (mathematical study of the forms -in topologic sense-), they are used to include his conjecture, that specifies that :…..” any closed curve content in a closed space -any be its initial form –of 3 or more dimensions- can be compressed in continuous way (reversible), toward a point, of way such that the space be deformed to a sphere, without holes”……Since the conjecture was formulated for Poincaré (1904), until now, various failed intents have existed (Poincare, Whitehead) and other general approximations (Freeman, Zeeman, Smale, Perelman, etc.), tending toward establishing the demonstrative algebraic formulae of these interconvertions, without achieving full acceptance of the mathematical world community.
Now it happens that 2 chinese scientific : Zhu Ziping and Cao Huaidong of the http://news3.xinhuanet.com/english/2006-06/04/content_4644754.htm universities of Zhougshan and Pennsylvania, finally have managed to establish the formulae. If these -contents in http://www.intlpress.com/AJM/AJM-v10.php 300 pages- receive the approval, of the respective scientific communities, notable advances in the fields of physics and engineering (buildings or ornamental structures that mutated toward or another form by means of technological factors, creation of chemical isomeric to will, discovery of the most adequate routes to enter and to leave wormholes, facilitating travel spatial, etc.), are expected.
But the bases of these interconvertions (chaos to order and vice versa), –that later will influence in the equations of Riemann- have deep roots in the works of another French: Jean Victor Poncelet (1812). He, aligning many disorganized not Euclidean visions (geometric forms views to distance), discovered a new mathematical branch: the proyective geometry. Then, when the eye sight to a pyramid that contains an apparently chaotic disposition of letters of colors, its see an orderly model, owed to the angle in which the chaos is projected, since the space to the eye.
De espacio caóticos a ordenados y, viceversa.
Cuando algunos historiadores matemáticos sustentan que Henri Poincaré es uno de los fundadores de la Topologia (estudio matemático de las formas -en sentido topológico-), suelen hacerlo incluyendo su conjetura,, que especifica que :…..” cualquier curva cerrada contenida en un espacio cerrado -cualquiera sea su forma inicial- de 3 o más dimensiones puede ser comprimida de modo continuo (reversible), hacia un punto, de modo tal que el espacio sea deformado a una esfera, sin agujeros”……Desde que se formuló la Conjetura de Poincaré (1904), a la fecha, han existido varios intentos frustros (Poincare, Whitehead) y otros aproximativos generales (Freeman, Zeeman, Smale, Perelman,etc), tendientes a establecer las fórmulas algebraicas demostrativas de estas interconversiones, sin lograr aceptación plena de la comunidad matemática mundial.
Ahora resulta que 2 chinos Zhu Ziping y Cao Huaidong de las universidades de Zhougshan y Pensilvania, han finalmente logrado establecer las fórmulas. Si éstas, contenidas en 300 páginas, reciben el Vo Bo, de las comunidades cientificas respectivas, se esperan avances notables en los campos de la fisica e ingenieria (edificios o estructuras ornamentales que mutaran hacia u otra forma mediante condicionantes tecnológicos, creación de isómeros quimicos a voluntad, descubrimiento de las rutas más adecuadas para ingresar y salir de agujeros de gusano, facilitando viajes espaciales, etc.
Pero los fundamentos de estas interconversiones (caos a orden y viceversa), –que más tarde inspirarian las ecuaciones de Riemann- tienen raices profundas en los trabajos de otro francés : Jean Victor Poncelet (1812). Este, al alinear muchas visiones no euclidianas desorganizadas (formas geométricas vistas a distancia), descubrió una nueva rama matemática: la geometría proyectiva. Asi, cuando el ojo mira a una pirámide que contiene una disposición aparentemente caótica de cartas de colores, vé un modelo ordenado, debido al ángulo en que se proyecta el caos, desde el espacio al ojo.
Now it happens that 2 chinese scientific : Zhu Ziping and Cao Huaidong of the http://news3.xinhuanet.com/english/2006-06/04/content_4644754.htm universities of Zhougshan and Pennsylvania, finally have managed to establish the formulae. If these -contents in http://www.intlpress.com/AJM/AJM-v10.php 300 pages- receive the approval, of the respective scientific communities, notable advances in the fields of physics and engineering (buildings or ornamental structures that mutated toward or another form by means of technological factors, creation of chemical isomeric to will, discovery of the most adequate routes to enter and to leave wormholes, facilitating travel spatial, etc.), are expected.
But the bases of these interconvertions (chaos to order and vice versa), –that later will influence in the equations of Riemann- have deep roots in the works of another French: Jean Victor Poncelet (1812). He, aligning many disorganized not Euclidean visions (geometric forms views to distance), discovered a new mathematical branch: the proyective geometry. Then, when the eye sight to a pyramid that contains an apparently chaotic disposition of letters of colors, its see an orderly model, owed to the angle in which the chaos is projected, since the space to the eye.
De espacio caóticos a ordenados y, viceversa.
Cuando algunos historiadores matemáticos sustentan que Henri Poincaré es uno de los fundadores de la Topologia (estudio matemático de las formas -en sentido topológico-), suelen hacerlo incluyendo su conjetura,, que especifica que :…..” cualquier curva cerrada contenida en un espacio cerrado -cualquiera sea su forma inicial- de 3 o más dimensiones puede ser comprimida de modo continuo (reversible), hacia un punto, de modo tal que el espacio sea deformado a una esfera, sin agujeros”……Desde que se formuló la Conjetura de Poincaré (1904), a la fecha, han existido varios intentos frustros (Poincare, Whitehead) y otros aproximativos generales (Freeman, Zeeman, Smale, Perelman,etc), tendientes a establecer las fórmulas algebraicas demostrativas de estas interconversiones, sin lograr aceptación plena de la comunidad matemática mundial.
Ahora resulta que 2 chinos Zhu Ziping y Cao Huaidong de las universidades de Zhougshan y Pensilvania, han finalmente logrado establecer las fórmulas. Si éstas, contenidas en 300 páginas, reciben el Vo Bo, de las comunidades cientificas respectivas, se esperan avances notables en los campos de la fisica e ingenieria (edificios o estructuras ornamentales que mutaran hacia u otra forma mediante condicionantes tecnológicos, creación de isómeros quimicos a voluntad, descubrimiento de las rutas más adecuadas para ingresar y salir de agujeros de gusano, facilitando viajes espaciales, etc.
Pero los fundamentos de estas interconversiones (caos a orden y viceversa), –que más tarde inspirarian las ecuaciones de Riemann- tienen raices profundas en los trabajos de otro francés : Jean Victor Poncelet (1812). Este, al alinear muchas visiones no euclidianas desorganizadas (formas geométricas vistas a distancia), descubrió una nueva rama matemática: la geometría proyectiva. Asi, cuando el ojo mira a una pirámide que contiene una disposición aparentemente caótica de cartas de colores, vé un modelo ordenado, debido al ángulo en que se proyecta el caos, desde el espacio al ojo.



.+Photo+Author.jpg)



1 Comments:
That's a great story. Waiting for more. » »
Post a Comment
<< Home